Representing signed numbers
by yaobin.wen
1. Number circle
In order to better understand the representations of signed numbers and their arithmetics, we need to have the concept of a “number circle.”
We all know what a “number line” is. Wikipedia provides the following explanation:
A number line is a graphical representation of a straight line that serves as spatial representation of numbers, usually graduated like a ruler with a particular origin point representing the number zero and evenly spaced marks in either direction representing integers, imagined to extend infinitely.
Because a number line is usually a straight line that doesn’t have boundaries, it can represent the numbers between \(-\infty\) and \(+\infty\).
However, on a computer, we don’t have unlimited amount of storage to represent infinity. When talking about number representation on computers, we need to focus on a \(N\)-bit storage where \(N\) is a positive integer such as 1, 2, 4, 8, etc. (Surely \(N\) can be any arbitrary positive integer such as 3 or 5. In fact, I’m going to use a 3-bit storage in the subsequent sections to talk about the signed number representation.)
Because \(N\) is a finite number, the smallest binary number it can represent is \((000\ldots0)_2\) where there are \(N\) 0s, and the largest binary number it can represent is \((111\ldots1)_2\) where there are \(N\) 1s. We can draw these binary numbers on a line segment which starts with \((000\ldots0)_2\) and ends with \((111\ldots1)_2\), as shown below:

However, if we are pointing at the largest number \((111\ldots1)_2\) and then move one position to the right, what will we get? Because moving one position towards the right direction means adding \(1\) to the previous number, moving one position to the right beyond the number \((111\ldots1)_2\) means adding \((1)_2\) to \((111\ldots1)_2\). “\((111\ldots1)_2 + 1\)” will cause overflow: the result is \((000\ldots0)_2\) and a carry bit \((1)_2\). But because we are talking about the \(N\)-bit storage here, we have to discard the carry bit \((1)_2\) because it doesn’t belong to any bit of this \(N\)-bit storage. As a result, the result of “\((111\ldots1)_2 + 1\)” is \((000\ldots0)_2\) again: we suddenly wrap around the right-most end of the line segment and go back to the left-most end of the line segment. This is similar to the “screen wraparound” in some early video games such as Asteroids. Because of this wraparound, it’s more accurate to use a “number circle” (see note below *) to represent the \(N\)-bit storage:
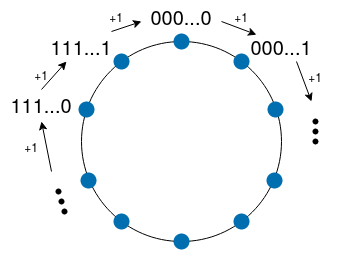
When \(N=3\), the number circle looks like as follows:
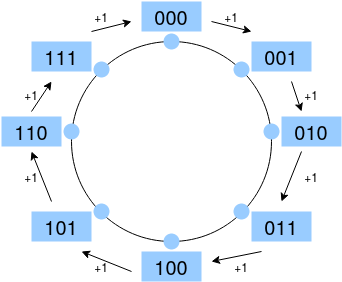
Note (*):
- I didn’t want to call it a “number ring” because it is already a term used in abstract algebra.
- The section Arithmetic on the Circle in Patterns for Beginning Programmers talks about something similar.
2. Encoding
All of the signed number representations that we talk about in this article are essentially methods of encoding abstract mathematical signed numbers into binaries.
Therefore, it makes sense to ask “What is the 4-bit sign-magnitude representation of \((7)_{10}\)?”, or “What is the 8-bit two’s complement representation of \((-3)_{10}\)?”. In these questions, we ask “how to encode abstract mathematical signed numbers \((7)_{10}\) and \((-3)_{10}\) into a specific binary form (i.e., 4-bit binary and 8-bit binary)”.
However, strictly speaking, it makes no sense to me to ask “What is the two’s complement representation of \((1101)_2\) which itself is in two’s complement representation?” because:
- “Two’s complement representation”, as we will see below, is a method of encoding numbers.
- Therefore, the question “What is the two’s complement representation of …” effectively asks how to encode a number into “two’s complement representation.”
- However, as we will see below, \((1101)_2\) is already the 4-bit two’s complement representation for the signed number \(-3\). In other words, \((1101)_2\) is already in the encoded form.
- Therefore, it makes no sense to me to ask “how to encode an encoded form.” (Instead, we can ask “how to decode \((1101)_2\).” But to answer this question, we need to know the encoding method that produced \((1101)_2\).)
- However, the question can be rephrased in two ways to make sense:
- Ask about decoding, the opposite process of encoding: “How to decode \((1101)_2\) that was encoded in two’s complement representation?”
- Ask about a different encoding method: “How to encode the two’s complement representation \((1101)_2\) in sign-magnitude?”
However, sometimes when we ask “What is the two’s complement representation of \((1101)_2\) which itself is in two’s complement representation?”, we are actually asking “The two’s complement representation \((1101)_2\) represents the number \((-3)_{10}\). What is the two’s complement representation of \((-3)_{10}\)’s additive inverse, i.e., \((3)_{10}\)?” The answer is \((0011)_2\). Personally, I find this way of asking question is confusing, so although I understand some people may ask this way, I still don’t prefer this kind of question.
3. Sign–magnitude
The first method of encoding mathematical numbers is the sign-magnitude representation. It is also called sign-and-magnitude or signed magnitude. For an \(N\)-bit storage, the most significant bit (MSb) is used to indicate the sign of the number:
- If MSb is 0, it’s a positive number.
- If MSb is 1, it’s a negative number.
The remaining \(N-1\) bits are used to represent the magnitude (aka “absolute value”) of the number.
For example, when \(N=3\):
| Binary | Sign | Magnitude | Signed decimal |
|---|---|---|---|
| \((000)_2\) | + | \((00)_2\) | \((+0)_{10}\) |
| \((001)_2\) | + | \((01)_2\) | \((+1)_{10}\) |
| \((010)_2\) | + | \((10)_2\) | \((+2)_{10}\) |
| \((011)_2\) | + | \((11)_2\) | \((+3)_{10}\) |
| \((100)_2\) | - | \((00)_2\) | \((-0)_{10}\) |
| \((101)_2\) | - | \((01)_2\) | \((-1)_{10}\) |
| \((110)_2\) | - | \((10)_2\) | \((-2)_{10}\) |
| \((111)_2\) | - | \((11)_2\) | \((-3)_{10}\) |
The number circle for the 3-bit storage is as follows:
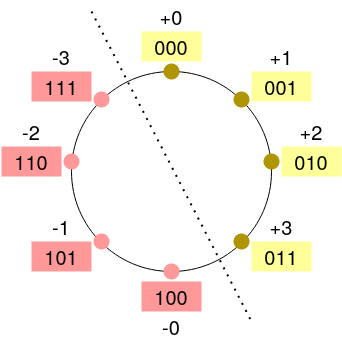
The advantage of the sign-magnitude representation is that it has an intuitive mapping to how we represent signed decimal numbers in everyday use, because in our daily life we also use the sign-magnitude representation to denote decimal numbers. For example, to represent the value “positive ten”, we simply write down the symbol + followed by the decimal magnitude 10; if we want to represent the value “negative ten”, we simply write down the symbol - followed by the decimal magnitude 10.
However, the sign-magnitude representation has drawbacks too:
- The value zero has two representations: positive zero and negative zero. Mathematically, the positive zero and the negative zero are the same thing. But because they have different binary representations, they must be treated differently in order to be interpreted as the value zero. This may make the hardware or software design more complicated.
- Addition requires different behaviors depending on the sign bit.
- Comparison requires inspecting the sign bit.
3.1 Addition
Adding signed numbers in sign-magnitude representation requires handling the signs explicitly and performing magnitude addition or subtraction based on the signs.
When the two numbers have the same signs (either both positive or both negative), adding them only needs to add the magnitudes and preserve the sign bit in the result. For example:
- \((001)_2 + (010)_2 = (011)_2\)
- The sign bits are both \(0\). Adding \((01)_2\) and \((10)_2\) results in \((11)_2\) without any carry bit. So the result is \((011)_2\).
- On the number circle, this addition means moving \((10)_2 = (2)_{10}\) positions to the right from \((001)_2\) to end up at \((011)_2\).
- \((100)_2 + (111)_2 = (111)_2\)
- The sign bits are both \(1\). Adding \((00)_2\) and \((11)_2\) results in \((11)_2\) without any carry bit. So the result is \((111)_2\).
- On the number circle, this addition means moving \((11)_2 = (3)_{10}\) positions to the right from \((100)_2\) to end up at \((111)_2\).
In the case of same signs, if the addition of the magnitudes produces a carry bit in the most significant bits, this indicates an overflow or underflow, i.e., the addition exceeds the largest number or the smallest number that these \(N\) bits can describe. Unfortunately, I haven’t found the documents about how to handle the overflow, possibly because sign-magnitude representation has become much less popular so the related information is no longer that available than the early days. However, by thinking about it, I think it’s up to the hardware/software designer to decide how to handle it, and there can be three ways:
- Treating an overflow as an error that possibly cause the machine to halt.
- Overflow on the positive half or the negative half on the number circle. This can be done by simply discarding the carry bit and preserve the sign bit.
- Overflow on the entire number circle. This can be done by adding the carry bit to the sum of the sign bits but discarding any carry bit that’s produced by the sum of the sign bits.
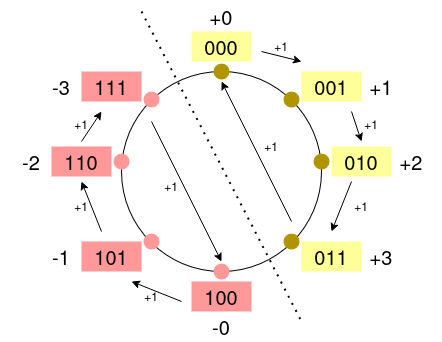
In this article, I’m going to use the second way: Overflow on the positive half or the negative half on the number circle. For example:
- \((001)_2 + (011)_2 = (000)_2\)
- The sign bits are both \(0\). Adding \((01)_2\) and \((11)_2\) results in \((00)_2\) with a carry bit \(1\). We need to discard the carry bit and keep the sign bit, so the result is \((000)_2\). On the number circle, this addition means, on the positive half of the number circle, moving \((11)_2 = (3)_{10}\) positions to the right from \((001)_2\) to end up at \((000)_2\).
- \((111)_2 + (111)_2 = (110)_2\)
- The sign bits are both \(1\). Adding \((11)_2\) and \((11)_2\) results in \((10)_2\) with a carry bit \(1\). We need to discard the carry bit and keep the sign bit, so the result is \((110)_2\). On the number circle, this addition means, on the negative half of the number circle, moving \((11)_2 = (3)_{10}\) positions to the right from \((111)_2\) to end up at \((110)_2\).
This can be illustrated as follows:
When the two numbers have different signs (i.e., one positive and one negative), adding them is done as follows:
- Compare the magnitudes of the two numbers and find the larger one and the smaller one.
- Subtract the smaller magnitude from the larger magnitude.
- Use the sign of the number with the larger magnitude for the result. If the magnitude parts are equal, use the positive sign.
Because zero has two sign-magnitude representations, we also need to handle zero specially, possibly by normalizing the result to always using \(0\).
3.2 Addition using sign-magnitude
The following table deals with overflow/underflow in the second way, i.e., overflowing/underflowing in the positive/negative half of the number circle.
| Addend | Addend | Sum | Carry bits (*) | Decimal | Over-/underflow | Note |
|---|---|---|---|---|---|---|
| \((000)_2\) | \((000)_2\) | \((000)_2\) | \((00x)_2\) | \(0 + 0 = 0\) | N/A | |
| \((000)_2\) | \((001)_2\) | \((001)_2\) | \((00x)_2\) | \(0 + 1 = 1\) | N/A | |
| \((000)_2\) | \((010)_2\) | \((010)_2\) | \((00x)_2\) | \(0 + 2 = 2\) | N/A | |
| \((000)_2\) | \((011)_2\) | \((011)_2\) | \((00x)_2\) | \(0 + 3 = 3\) | N/A | |
| \((000)_2\) | \((100)_2\) | \((000)_2\) | \((00x)_2\) | \(0 + (-0) = 0\) | N/A | Normalized to \(0\). |
| \((000)_2\) | \((101)_2\) | \((101)_2\) | \((00x)_2\) | \(0 + (-1) = -1\) | N/A | |
| \((000)_2\) | \((110)_2\) | \((110)_2\) | \((00x)_2\) | \(0 + (-2) = -2\) | N/A | |
| \((000)_2\) | \((111)_2\) | \((111)_2\) | \((00x)_2\) | \(0 + (-3) = -3\) | N/A | |
| \((001)_2\) | \((001)_2\) | \((010)_2\) | \((01x)_2\) | \(1 + 1 = 2\) | N/A | |
| \((001)_2\) | \((010)_2\) | \((011)_2\) | \((00x)_2\) | \(1 + 2 = 3\) | N/A | |
| \((001)_2\) | \((011)_2\) | \((000)_2\) | \((11x)_2\) | \(1 + 3 = 0\) | Overflow | (1) |
| \((001)_2\) | \((100)_2\) | \((001)_2\) | \((00x)_2\) | \(1 + (-0) = 1\) | N/A | |
| \((001)_2\) | \((101)_2\) | \((000)_2\) | \((01x)_2\) | \(1 + (-1) = 0\) | N/A | |
| \((001)_2\) | \((110)_2\) | \((101)_2\) | \((00x)_2\) | \(1 + (-2) = -1\) | N/A | |
| \((001)_2\) | \((111)_2\) | \((110)_2\) | \((11x)_2\) | \(1 + (-3) = -2\) | N/A | |
| \((010)_2\) | \((010)_2\) | \((000)_2\) | \((10x)_2\) | \(2 + 2 = 0\) | Overflow | (2) |
| \((010)_2\) | \((011)_2\) | \((001)_2\) | \((10x)_2\) | \(2 + 3 = 1\) | Overflow | (3) |
| \((010)_2\) | \((100)_2\) | \((010)_2\) | \((00x)_2\) | \(2 + (-0) = 2\) | N/A | |
| \((010)_2\) | \((101)_2\) | \((001)_2\) | \((00x)_2\) | \(2 + (-1) = 1\) | N/A | |
| \((010)_2\) | \((110)_2\) | \((000)_2\) | \((10x)_2\) | \(2 + (-2) = 0\) | N/A | |
| \((010)_2\) | \((111)_2\) | \((101)_2\) | \((10x)_2\) | \(2 + (-3) = -1\) | N/A | |
| \((011)_2\) | \((011)_2\) | \((010)_2\) | \((11x)_2\) | \(3 + 3 = 2\) | Overflow | (4) |
| \((011)_2\) | \((100)_2\) | \((011)_2\) | \((00x)_2\) | \(3 + (-0) = 3\) | N/A | |
| \((011)_2\) | \((101)_2\) | \((010)_2\) | \((11x)_2\) | \(3 + (-1) = 2\) | N/A | |
| \((011)_2\) | \((110)_2\) | \((001)_2\) | \((10x)_2\) | \(3 + (-2) = 1\) | N/A | |
| \((011)_2\) | \((111)_2\) | \((000)_2\) | \((11x)_2\) | \(3 + (-3) = 0\) | N/A | |
| \((100)_2\) | \((100)_2\) | \((000)_2\) | \((00x)_2\) | \(-0 + (-0) = 0\) | N/A | Normalized to \(0\). |
| \((100)_2\) | \((101)_2\) | \((101)_2\) | \((00x)_2\) | \(-0 + (-1) = -1\) | N/A | |
| \((100)_2\) | \((110)_2\) | \((110)_2\) | \((00x)_2\) | \(-0 + (-2) = -2\) | N/A | |
| \((100)_2\) | \((111)_2\) | \((111)_2\) | \((00x)_2\) | \(-0 + (-3) = -3\) | N/A | |
| \((101)_2\) | \((101)_2\) | \((110)_2\) | \((01x)_2\) | \(-1 + (-1) = -2\) | N/A | |
| \((101)_2\) | \((110)_2\) | \((111)_2\) | \((00x)_2\) | \(-1 + (-2) = -3\) | N/A | |
| \((101)_2\) | \((111)_2\) | \((100)_2\) | \((11x)_2\) | \(-1 + (-3) = -0\) | Underflow | (5) |
| \((110)_2\) | \((110)_2\) | \((100)_2\) | \((10x)_2\) | \(-2 + (-2) = -0\) | Underflow | (6) |
| \((110)_2\) | \((111)_2\) | \((101)_2\) | \((10x)_2\) | \(-2 + (-3) = -1\) | Underflow | (7) |
| \((111)_2\) | \((111)_2\) | \((110)_2\) | \((11x)_2\) | \(-3 + (-3) = -2\) | Underflow | (8) |
Note (*):
- The
xmeans “no carry bit for the addition of the first bits in the two numbers” because in the table above, we only add two numbers. If we add more than two numbers, the adding of the previous two numbers may produce a carry bit that should be added to the next number.
Notes:
- (1) ~ (8): In the cases of over- or underflow, we overflow or underflow in half of the number circle.
- (5)(6): Frankly speaking, in the case of underflow, I don’t know if I should normalize the result to \(0\) or just keep whatever is produced from the addition.
4. One’s complement
In a \(N\)-bit one’s complement representation:
- The most significant bit (MSb) indicates the sign of the number:
0means a positive number.1means a negative number.
- For positive numbers, the remaining \(N-1\) bits are still the magnitude of the number. In fact, for positive numbers, their one’s complement representation is the same as the binary numbers themselves.
- For negative number, the remaining \(N-1\) bits are not the magnitude of the number but the inversion of the \(N-1\) bits of the corresponding positive numbers.
For example, when \(N=3\):
| Binary | Sign | Signed decimal |
|---|---|---|
| \((000)_2\) | + | \((+0)_{10}\) |
| \((001)_2\) | + | \((+1)_{10}\) |
| \((010)_2\) | + | \((+2)_{10}\) |
| \((011)_2\) | + | \((+3)_{10}\) |
| \((100)_2\) | - | \((-3)_{10}\) |
| \((101)_2\) | - | \((-2)_{10}\) |
| \((110)_2\) | - | \((-1)_{10}\) |
| \((111)_2\) | - | \((-0)_{10}\) |
Take \((010)_2\) and \((101)_2\) for examples:
- \((010)_2\) is a positive number because its MSb is \(0\).
- The remaining 2 bits \((10)_2\) are the magnitude, so the value is \((2)_{10}\).
- \((101)_2\) is a negative number because its MSb is \(1\).
- The remaining 2 bits \((01)_2\) are the inversion of \((10)_2\), so \((01)_2\) indicates the value \((2)_{10}\) under one’s complement. As a result, \((101)_2\) indicates \((-2)_{10}\).
Note that zero still has two representations: \((000)_2\) and \((111)_2\).
The number circle is as follows:
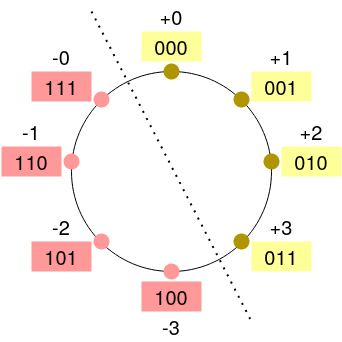
4.1 Addition using one’s complement
Adding two binaries in one’s complement is straightforward. Simply align the values on the least significant bit and add them bit by bit, propagating any carry to the bit one position left. If the carry extends past the end of the word it is said to have “wrapped around”, a condition called an “end-around carry”. When this occurs, the bit must be added back in at the right-most bit.
This adding arithmetics implements the clockwise rotation on the number circle (except at \((111)_2\)). For example:
- \((000)_2 + (010)_2\) means rotating two positions from \((000)_2\) to get the correct result \((010)_2\).
- \((011)_2 + (001)_2\) means rotating one position from \((011)_2\) to get the overflowed result \((100)_2\).
- Specially, \((111)_2 + (001)_2\) means rotating two positions from \((111)_2\) to get the correct result \((001)_2\). The reason is \((111)_2\) and \((000)_2\) are mathematically equivalent, so adding a number to \((111)_2\) should produce the same result as adding the same number to \((000)_2\).
Here are the addition of 3-bit binaries in one’s complement:
| Addend | Addend | Sum | Decimal | Note |
|---|---|---|---|---|
| \((000)_2\) | \((000)_2\) | \((000)_2\) | \(0 + 0 = 0\) | |
| \((000)_2\) | \((001)_2\) | \((001)_2\) | \(0 + 1 = 0\) | |
| \((000)_2\) | \((010)_2\) | \((010)_2\) | \(0 + 2 = 2\) | |
| \((000)_2\) | \((011)_2\) | \((011)_2\) | \(0 + 3 = 2\) | |
| \((000)_2\) | \((100)_2\) | \((100)_2\) | \(0 + (-3) = -3\) | |
| \((000)_2\) | \((101)_2\) | \((101)_2\) | \(0 + (-2) = -2\) | |
| \((000)_2\) | \((110)_2\) | \((110)_2\) | \(0 + (-1) = -1\) | |
| \((000)_2\) | \((111)_2\) | \((111)_2\) | \(0 + (-0) = -0\) | |
| \((001)_2\) | \((000)_2\) | \((001)_2\) | \(1 + 0 = 1\) | |
| \((001)_2\) | \((001)_2\) | \((010)_2\) | \(1 + 1 = 2\) | |
| \((001)_2\) | \((010)_2\) | \((011)_2\) | \(1 + 2 = 3\) | |
| \((001)_2\) | \((011)_2\) | \((100)_2\) | \(1 + 3 = -3\) | Overflow |
| \((001)_2\) | \((100)_2\) | \((101)_2\) | \(1 + (-3) = -2\) | |
| \((001)_2\) | \((101)_2\) | \((110)_2\) | \(1 + (-2) = -1\) | |
| \((001)_2\) | \((110)_2\) | \((111)_2\) | \(1 + (-1) = -0\) | |
| \((001)_2\) | \((111)_2\) | \((001)_2\) | \(1 + (-0) = 1\) | (1) |
| \((010)_2\) | \((000)_2\) | \((010)_2\) | \(2 + 0 = 2\) | |
| \((010)_2\) | \((001)_2\) | \((011)_2\) | \(2 + 1 = 3\) | |
| \((010)_2\) | \((010)_2\) | \((100)_2\) | \(2 + 2 = -3\) | Overflow |
| \((010)_2\) | \((011)_2\) | \((101)_2\) | \(2 + 3 = -2\) | Overflow |
| \((010)_2\) | \((100)_2\) | \((110)_2\) | \(2 + (-3) = -1\) | |
| \((010)_2\) | \((101)_2\) | \((111)_2\) | \(2 + (-2) = -0\) | |
| \((010)_2\) | \((110)_2\) | \((001)_2\) | \(2 + (-1) = 1\) | (2) |
| \((010)_2\) | \((111)_2\) | \((010)_2\) | \(2 + (-0) = 2\) | |
| \((011)_2\) | \((000)_2\) | \((011)_2\) | \(3 + 0 = 3\) | |
| \((011)_2\) | \((001)_2\) | \((100)_2\) | \(3 + 1 = -3\) | Overflow |
| \((011)_2\) | \((010)_2\) | \((101)_2\) | \(3 + 2 = -2\) | Overflow |
| \((011)_2\) | \((011)_2\) | \((110)_2\) | \(3 + 3 = -1\) | Overflow |
| \((011)_2\) | \((100)_2\) | \((111)_2\) | \(3 + (-3) = -0\) | |
| \((011)_2\) | \((101)_2\) | \((001)_2\) | \(3 + (-2) = 1\) | (3) |
| \((011)_2\) | \((110)_2\) | \((010)_2\) | \(3 + (-1) = 2\) | (4) |
| \((011)_2\) | \((111)_2\) | \((011)_2\) | \(3 + (-0) = 3\) | (5) |
| \((100)_2\) | \((000)_2\) | \((100)_2\) | \(-3 + 0 = -3\) | |
| \((100)_2\) | \((001)_2\) | \((101)_2\) | \(-3 + 1 = -2\) | |
| \((100)_2\) | \((010)_2\) | \((110)_2\) | \(-3 + 2 = -1\) | |
| \((100)_2\) | \((011)_2\) | \((111)_2\) | \(-3 + 3 = -0\) | |
| \((100)_2\) | \((100)_2\) | \((001)_2\) | \(-3 + (-3) = 1\) | (6) Underflow |
| \((100)_2\) | \((101)_2\) | \((010)_2\) | \(-3 + (-2) = 2\) | (7) Underflow |
| \((100)_2\) | \((110)_2\) | \((011)_2\) | \(-3 + (-1) = 3\) | (8) Underflow |
| \((100)_2\) | \((111)_2\) | \((100)_2\) | \(-3 + (-0) = -3\) | (9) |
| \((101)_2\) | \((000)_2\) | \((101)_2\) | \(-2 + 0 = -2\) | |
| \((101)_2\) | \((001)_2\) | \((110)_2\) | \(-2 + 1 = -1\) | |
| \((101)_2\) | \((010)_2\) | \((111)_2\) | \(-2 + 2 = -0\) | |
| \((101)_2\) | \((011)_2\) | \((001)_2\) | \(-2 + 3 = 1\) | (10) |
| \((101)_2\) | \((100)_2\) | \((010)_2\) | \(-2 + (-3) = 2\) | (11) Underflow |
| \((101)_2\) | \((101)_2\) | \((011)_2\) | \(-2 + (-2) = 3\) | (12) Underflow |
| \((101)_2\) | \((110)_2\) | \((100)_2\) | \(-2 + (-1) = -3\) | (13) |
| \((101)_2\) | \((111)_2\) | \((101)_2\) | \(-2 + (-0) = -2\) | (14) |
| \((110)_2\) | \((000)_2\) | \((110)_2\) | \(-1 + 0 = -1\) | |
| \((110)_2\) | \((001)_2\) | \((111)_2\) | \(-1 + 1 = -0\) | |
| \((110)_2\) | \((010)_2\) | \((001)_2\) | \(-1 + 2 = 1\) | (15) |
| \((110)_2\) | \((011)_2\) | \((010)_2\) | \(-1 + 3 = 2\) | (16) |
| \((110)_2\) | \((100)_2\) | \((011)_2\) | \(-1 + (-3) = 3\) | (17) Underflow |
| \((110)_2\) | \((101)_2\) | \((100)_2\) | \(-1 + (-2) = -3\) | (18) |
| \((110)_2\) | \((110)_2\) | \((101)_2\) | \(-1 + (-1) = -2\) | (19) |
| \((110)_2\) | \((111)_2\) | \((110)_2\) | \(-1 + (-0) = -1\) | (20) |
| \((111)_2\) | \((000)_2\) | \((111)_2\) | \(-0 + 0 = -0\) | |
| \((111)_2\) | \((001)_2\) | \((001)_2\) | \(-0 + 1 = 1\) | (21) |
| \((111)_2\) | \((010)_2\) | \((010)_2\) | \(-0 + 2 = 2\) | (22) |
| \((111)_2\) | \((011)_2\) | \((011)_2\) | \(-0 + 3 = 3\) | (23) |
| \((111)_2\) | \((100)_2\) | \((100)_2\) | \(-0 + (-3) = -3\) | (24) |
| \((111)_2\) | \((101)_2\) | \((101)_2\) | \(-0 + (-2) = -2\) | (25) |
| \((111)_2\) | \((110)_2\) | \((110)_2\) | \(-0 + (-1) = -1\) | (26) |
| \((111)_2\) | \((111)_2\) | \((111)_2\) | \(-0 + (-0) = -0\) | (27) |
Notes:
- (1) \((001)_2 + (111)_2 = (000)_2\) with carry bit 1. Add this carry bit back to the least significant bit (LSb) of \((000)_2\) can produce the correct result \((001)_2\).
- Explanation: \((111)_2\) is minus zero (\(-0\)), so \((001)_2\) plus minus zero should still be \((001)_2\) itself.
- (2) \((010)_2 + (110)_2 = (001)_2\) with carry bit 1. Add this carry bit back to the LSb of \((001)_2\) can produce the correct result \((010)_2\).
- (3) \((011)_2 + (101)_2 = (000)_2\) with carry bit 1. Add this carry bit back to the LSb of \((000)_2\) can produce the correct result \((001)_2\).
- (4) \((011)_2 + (110)_2 = (001)_2\) with carry bit 1. Add this carry bit back to the LSb of \((001)_2\) can produce the correct result \((010)_2\).
- (5) \((011)_2 + (111)_2 = (010)_2\) with carry bit 1. Add this carry bit back to the LSb of \((010)_2\) can produce the correct result \((011)_2\).
- (6) \((100)_2 + (100)_2 = (000)_2\) with carry bit 1. Add this carry bit back to the LSb of \((000)_2\) can produce the correct result \((001)_2\).
- This is also a case of underflow. The mathematically correct answer should be \((-6)_{10}\). However, \((-6)_{10}\) cannot be represented by 3 bits in one’s complement.
- (7) \((100)_2 + (101)_2 = (001)_2\) with carry bit 1. Add this carry bit back to the LSb of \((001)_2\) can produce the correct result \((010)_2\).
- This is also a case of underflow. The mathematically correct answer should be \((-5)_{10}\). However, \((-5)_{10}\) cannot be represented by 3 bits in one’s complement.
- (8) \((100)_2 + (110)_2 = (010)_2\) with carry bit 1. Add this carry bit back to the LSb of \((010)_2\) can produce the correct result \((011)_2\).
- This is also a case of underflow. The mathematically correct answer should be \((-4)_{10}\). However, \((-4)_{10}\) cannot be represented by 3 bits in one’s complement.
- (9) \((100)_2 + (111)_2 = (011)_2\) with carry bit 1. Add this carry bit back to the LSb of \((011)_2\) can produce the correct result \((100)_2\).
- (10) \((101)_2 + (011)_2 = (000)_2\) with carry bit 1. Add this carry bit back to the LSb of \((000)_2\) can produce the correct result \((001)_2\).
- (11) \((101)_2 + (100)_2 = (001)_2\) with carry bit 1. Add this carry bit back to the LSb of \((001)_2\) can produce the correct result \((010)_2\).
- This is also a case of underflow. The mathematically correct answer should be \((-5)_{10}\). However, \((-5)_{10}\) cannot be represented by 3 bits in one’s complement.
- (12) \((101)_2 + (101)_2 = (010)_2\) with carry bit 1. Add this carry bit back to the LSb of \((010)_2\) can produce the correct result \((011)_2\).
- This is also a case of underflow. The mathematically correct answer should be \((-4)_{10}\). However, \((-4)_{10}\) cannot be represented by 3 bits in one’s complement.
- (13) \((101)_2 + (110)_2 = (011)_2\) with carry bit 1. Add this carry bit back to the LSb of \((011)_2\) can produce the correct result \((100)_2\).
- (14) \((101)_2 + (111)_2 = (100)_2\) with carry bit 1. Add this carry bit back to the LSb of \((100)_2\) can produce the correct result \((101)_2\).
- (15) \((110)_2 + (010)_2 = (000)_2\) with carry bit 1. Add this carry bit back to the LSb of \((000)_2\) can produce the correct result \((001)_2\).
- (16) \((110)_2 + (011)_2 = (001)_2\) with carry bit 1. Add this carry bit back to the LSb of \((001)_2\) can produce the correct result \((010)_2\).
- (17) \((110)_2 + (100)_2 = (010)_2\) with carry bit 1. Add this carry bit back to the LSb of \((010)_2\) can produce the correct result \((011)_2\).
- This is also a case of underflow. The mathematically correct answer should be \((-4)_{10}\). However, \((-4)_{10}\) cannot be represented by 3 bits in one’s complement.
- (18) \((110)_2 + (101)_2 = (011)_2\) with carry bit 1. Add this carry bit back to the LSb of \((011)_2\) can produce the correct result \((100)_2\).
- (19) \((110)_2 + (110)_2 = (100)_2\) with carry bit 1. Add this carry bit back to the LSb of \((100)_2\) can produce the correct result \((101)_2\).
- (20) \((110)_2 + (111)_2 = (101)_2\) with carry bit 1. Add this carry bit back to the LSb of \((101)_2\) can produce the correct result \((110)_2\).
- (21) \((111)_2 + (001)_2 = (000)_2\) with carry bit 1. Add this carry bit back to the LSb of \((000)_2\) can produce the correct result \((001)_2\).
- (22) \((111)_2 + (010)_2 = (001)_2\) with carry bit 1. Add this carry bit back to the LSb of \((001)_2\) can produce the correct result \((010)_2\).
- (23) \((111)_2 + (011)_2 = (010)_2\) with carry bit 1. Add this carry bit back to the LSb of \((010)_2\) can produce the correct result \((011)_2\).
- (24) \((111)_2 + (100)_2 = (011)_2\) with carry bit 1. Add this carry bit back to the LSb of \((011)_2\) can produce the correct result \((100)_2\).
- (25) \((111)_2 + (101)_2 = (100)_2\) with carry bit 1. Add this carry bit back to the LSb of \((100)_2\) can produce the correct result \((101)_2\).
- (26) \((111)_2 + (110)_2 = (101)_2\) with carry bit 1. Add this carry bit back to the LSb of \((101)_2\) can produce the correct result \((110)_2\).
- (27) \((111)_2 + (111)_2 = (110)_2\) with carry bit 1. Add this carry bit back to the LSb of \((110)_2\) can produce the correct result \((111)_2\).
4.2 Subtraction using one’s complement
Subtraction can be implemented by adding the negative counterpart. For example:
- \((2)_{10} - (1)_{10} = (2)_{10} + (-1)_{10} = (010)_2 + (110)_2 = (001)_2 = (1)_{10}\)
- \((-1)_{10} - (2)_{10} = (-1)_{10} + (-2)_{10} = (110)_2 + (101)_2 = (100)_2 = (-3)_{10}\)
- \((1)_{10} - (-2)_{10} = (1)_{10} + (2)_{10} = (001)_2 + (010)_2 = (011)_2 = (3)_{10}\)
However, the subtraction can also be directly calculated this way: Align the values on the least significant bit and subtract, propagating any borrow to the bit one position left. If the borrow extends past the end of the word it is said to have “wrapped around”, a condition called an “end-around borrow”. When this occurs, the bit must be subtracted from the right-most bit to get the correct result.
5. Two’s complement
In two’s complement representation:
- We still use the most significant bit (MSb) to indicate the sign of the number:
0means a positive number.1means a negative number.
- For positive numbers, the remaining \(N-1\) bits are still the magnitude of the number. In fact, for positive numbers, their representations in two’s complement, one’s complement, and signed magnitude are the same.
- For negative numbers, the two’s complement can be obtained in this way:
- Get the corresponding positive number. For example, if we want to figure out the two’s complement of \(-1\), then firstly get the corresponding positive number \(+1\).
- Flip all the bits: \(0 \rightarrow 1\) or \(1 \rightarrow 0\).
- Add one to the result.
- Discard any carry bit at the most significant big, if needed.
For example,
- The two’s complement representation of \((+3)_{10}\) is \((011)_2\).
- To get the two’s complement representation of \((-3)_{10}\), we can follow the steps below:
- Get the corresponding positive number which is \((+3)_{10} = (011)_2\).
- Flip all the bits of \((011)_2\) to get \((100)_2\).
- Add one to the result \((100)_2\) to get \((101)_2\).
- No need to discard any carry bit.
- So the two’s complement representation of \((-3)_{10}\) is \((101)_2\).
For a 3-bit system, we can encode the 8 numbers differently (Range: \([-4, 3]\))::
| Binary | Sign | Signed decimal |
|---|---|---|
| \((000)_2\) | + | \((0)_{10}\) |
| \((001)_2\) | + | \((1)_{10}\) |
| \((010)_2\) | + | \((2)_{10}\) |
| \((011)_2\) | + | \((3)_{10}\) |
| \((100)_2\) | - | \((-4)_{10}\) |
| \((101)_2\) | - | \((-3)_{10}\) |
| \((110)_2\) | - | \((-2)_{10}\) |
| \((111)_2\) | - | \((-1)_{10}\) |
The number circle is as follows:
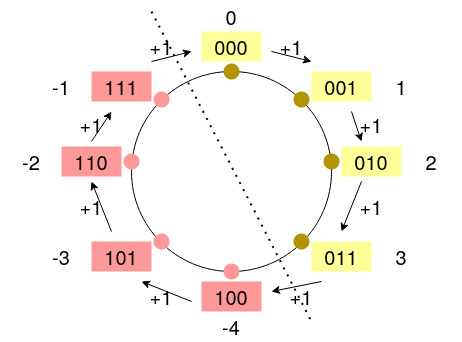
Another way of finding a number’s two complement is: Work right-to-left and write down all digits through when you reach a 1. Then invert the rest of the digits. For example:
- 1). The original number is \((0010)_2 = (2)_{10}\).
- 2). Work right to left and write down all digits through until reaching a
1:??10. - 3). Invert the rest of the digits: \((1110)_2 = (-2)_{10}\).
5.1 Converting a binary in two’s complement to decimal
Because the most significant bit (MSb) of a binary in two’s complement indicates the sign of the number, when converted to the corresponding decimal number, the value of the sign bit should be positive or negative accordingly. For example:
- \((0110)_2 = [(+0) \times 2^3] + (1 \times 2^2) + (1 \times 2^1) + (0 \times 2^0) = (0)_{10} + (4)_{10} + (2)_{10} + (0)_{10} = (6)_{10}\)
- \((1010)_2 = [(-1) \times 2^3] + (0 \times 2^2) + (1 \times 2^1) + (0 \times 2^0) = (-8)_{10} + (0)_{10} + (2)_{10} + (0)_{10} = (-6)_{10}\)
5.2 Addition using two’s complement
Adding two’s complement numbers requires no special processing even if the operands have opposite signs; the sign of the result is determined automatically. However, the sum may not be valid when an overflow or underflow happens. An overflow/underflow can be determined by the left-most two bits of the carry bits: if they are the same (i.e., both are 0 or both are 1), then no overflow/underflow happens; if they are different (i.e., either 01 or 10), then an overflow/underflow happens.
Here are the addition of 3-bit binaries in two’s complement. The carry bits consist of four bits but the first bit, indicated by x, is not meaningful in this context because the first bits of the two addends don’t receive any carry bit.
| Addend | Addend | Sum | Carry bits | Decimal | Over-/underflow | Note |
|---|---|---|---|---|---|---|
| \((000)_2\) | \((000)_2\) | \((000)_2\) | \((000x)_2\) | \(0 + 0 = 0\) | ||
| \((000)_2\) | \((001)_2\) | \((001)_2\) | \((000x)_2\) | \(0 + 1 = 0\) | ||
| \((000)_2\) | \((010)_2\) | \((010)_2\) | \((000x)_2\) | \(0 + 2 = 2\) | ||
| \((000)_2\) | \((011)_2\) | \((011)_2\) | \((000x)_2\) | \(0 + 3 = 2\) | ||
| \((000)_2\) | \((100)_2\) | \((100)_2\) | \((000x)_2\) | \(0 + (-4) = -4\) | ||
| \((000)_2\) | \((101)_2\) | \((101)_2\) | \((000x)_2\) | \(0 + (-3) = -3\) | ||
| \((000)_2\) | \((110)_2\) | \((110)_2\) | \((000x)_2\) | \(0 + (-2) = -2\) | ||
| \((000)_2\) | \((111)_2\) | \((111)_2\) | \((000x)_2\) | \(0 + (-1) = -1\) | ||
| \((001)_2\) | \((000)_2\) | \((001)_2\) | \((000x)_2\) | \(1 + 0 = 1\) | ||
| \((001)_2\) | \((001)_2\) | \((010)_2\) | \((001x)_2\) | \(1 + 1 = 2\) | ||
| \((001)_2\) | \((010)_2\) | \((011)_2\) | \((000x)_2\) | \(1 + 2 = 3\) | ||
| \((001)_2\) | \((011)_2\) | \((100)_2\) | \((011x)_2\) | \(1 + 3 = -4\) | Overflow | (1) |
| \((001)_2\) | \((100)_2\) | \((101)_2\) | \((000x)_2\) | \(1 + (-4) = -3\) | ||
| \((001)_2\) | \((101)_2\) | \((110)_2\) | \((001x)_2\) | \(1 + (-3) = -2\) | ||
| \((001)_2\) | \((110)_2\) | \((111)_2\) | \((000x)_2\) | \(1 + (-2) = -1\) | ||
| \((001)_2\) | \((111)_2\) | \((000)_2\) | \((111x)_2\) | \(1 + (-1) = 0\) | ||
| \((010)_2\) | \((000)_2\) | \((010)_2\) | \((000x)_2\) | \(2 + 0 = 2\) | ||
| \((010)_2\) | \((001)_2\) | \((011)_2\) | \((000x)_2\) | \(2 + 1 = 3\) | ||
| \((010)_2\) | \((010)_2\) | \((100)_2\) | \((010x)_2\) | \(2 + 2 = -4\) | Overflow | (2) |
| \((010)_2\) | \((011)_2\) | \((101)_2\) | \((010x)_2\) | \(2 + 3 = -3\) | Overflow | (3) |
| \((010)_2\) | \((100)_2\) | \((110)_2\) | \((000x)_2\) | \(2 + (-4) = -2\) | ||
| \((010)_2\) | \((101)_2\) | \((111)_2\) | \((000x)_2\) | \(2 + (-3) = -1\) | ||
| \((010)_2\) | \((110)_2\) | \((000)_2\) | \((110x)_2\) | \(2 + (-2) = 0\) | ||
| \((010)_2\) | \((111)_2\) | \((001)_2\) | \((110x)_2\) | \(2 + (-1) = 1\) | ||
| \((011)_2\) | \((000)_2\) | \((011)_2\) | \((000x)_2\) | \(3 + 0 = 3\) | ||
| \((011)_2\) | \((001)_2\) | \((100)_2\) | \((011x)_2\) | \(3 + 1 = -4\) | Overflow | (4) |
| \((011)_2\) | \((010)_2\) | \((101)_2\) | \((010x)_2\) | \(3 + 2 = -3\) | Overflow | (5) |
| \((011)_2\) | \((011)_2\) | \((110)_2\) | \((011x)_2\) | \(3 + 3 = -2\) | Overflow | (6) |
| \((011)_2\) | \((100)_2\) | \((111)_2\) | \((000x)_2\) | \(3 + (-4) = -1\) | ||
| \((011)_2\) | \((101)_2\) | \((000)_2\) | \((111x)_2\) | \(3 + (-3) = 0\) | ||
| \((011)_2\) | \((110)_2\) | \((001)_2\) | \((110x)_2\) | \(3 + (-2) = 1\) | ||
| \((011)_2\) | \((111)_2\) | \((010)_2\) | \((111x)_2\) | \(3 + (-1) = 2\) | ||
| \((100)_2\) | \((000)_2\) | \((100)_2\) | \((000x)_2\) | \(-4 + 0 = -4\) | ||
| \((100)_2\) | \((001)_2\) | \((101)_2\) | \((000x)_2\) | \(-4 + 1 = -3\) | ||
| \((100)_2\) | \((010)_2\) | \((110)_2\) | \((000x)_2\) | \(-4 + 2 = -2\) | ||
| \((100)_2\) | \((011)_2\) | \((111)_2\) | \((000x)_2\) | \(-4 + 3 = -1\) | ||
| \((100)_2\) | \((100)_2\) | \((000)_2\) | \((100x)_2\) | \(-4 + (-4) = 0\) | Underflow | (7) |
| \((100)_2\) | \((101)_2\) | \((001)_2\) | \((100x)_2\) | \(-4 + (-3) = 1\) | Underflow | (8) |
| \((100)_2\) | \((110)_2\) | \((010)_2\) | \((100x)_2\) | \(-4 + (-2) = 2\) | Underflow | (9) |
| \((100)_2\) | \((111)_2\) | \((011)_2\) | \((100x)_2\) | \(-4 + (-1) = 3\) | Underflow | (10) |
| \((101)_2\) | \((000)_2\) | \((101)_2\) | \((000x)_2\) | \(-3 + 0 = -3\) | ||
| \((101)_2\) | \((001)_2\) | \((110)_2\) | \((001x)_2\) | \(-3 + 1 = -2\) | ||
| \((101)_2\) | \((010)_2\) | \((111)_2\) | \((000x)_2\) | \(-3 + 2 = -1\) | ||
| \((101)_2\) | \((011)_2\) | \((000)_2\) | \((111x)_2\) | \(-3 + 3 = 0\) | ||
| \((101)_2\) | \((100)_2\) | \((001)_2\) | \((100x)_2\) | \(-3 + (-4) = 1\) | Underflow | (11) |
| \((101)_2\) | \((101)_2\) | \((010)_2\) | \((101x)_2\) | \(-3 + (-3) = 2\) | Underflow | (12) |
| \((101)_2\) | \((110)_2\) | \((011)_2\) | \((100x)_2\) | \(-3 + (-2) = 3\) | Underflow | (13) |
| \((101)_2\) | \((111)_2\) | \((100)_2\) | \((111x)_2\) | \(-3 + (-1) = -4\) | ||
| \((110)_2\) | \((000)_2\) | \((110)_2\) | \((000x)_2\) | \(-2 + 0 = -2\) | ||
| \((110)_2\) | \((001)_2\) | \((111)_2\) | \((000x)_2\) | \(-2 + 1 = -1\) | ||
| \((110)_2\) | \((010)_2\) | \((000)_2\) | \((110x)_2\) | \(-2 + 2 = 0\) | ||
| \((110)_2\) | \((011)_2\) | \((001)_2\) | \((110x)_2\) | \(-2 + 3 = 1\) | ||
| \((110)_2\) | \((100)_2\) | \((010)_2\) | \((100x)_2\) | \(-2 + (-4) = 2\) | Underflow | (14) |
| \((110)_2\) | \((101)_2\) | \((011)_2\) | \((100x)_2\) | \(-2 + (-3) = 3\) | Underflow | (15) |
| \((110)_2\) | \((110)_2\) | \((100)_2\) | \((110x)_2\) | \(-2 + (-2) = -4\) | ||
| \((110)_2\) | \((111)_2\) | \((101)_2\) | \((110x)_2\) | \(-2 + (-1) = -3\) | ||
| \((111)_2\) | \((000)_2\) | \((111)_2\) | \((000x)_2\) | \(-1 + 0 = -1\) | ||
| \((111)_2\) | \((001)_2\) | \((000)_2\) | \((111x)_2\) | \(-1 + 1 = 0\) | ||
| \((111)_2\) | \((010)_2\) | \((001)_2\) | \((110x)_2\) | \(-1 + 2 = 1\) | ||
| \((111)_2\) | \((011)_2\) | \((010)_2\) | \((111x)_2\) | \(-1 + 3 = 2\) | ||
| \((111)_2\) | \((100)_2\) | \((011)_2\) | \((100x)_2\) | \(-1 + (-4) = 3\) | Underflow | (16) |
| \((111)_2\) | \((101)_2\) | \((100)_2\) | \((111x)_2\) | \(-1 + (-3) = -4\) | ||
| \((111)_2\) | \((110)_2\) | \((101)_2\) | \((110x)_2\) | \(-1 + (-2) = -3\) | ||
| \((111)_2\) | \((111)_2\) | \((110)_2\) | \((111x)_2\) | \(-1 + (-1) = -2\) |
Notes:
- (1) ~ (6) are cases of overflow because the left-most two bits are
01and they are different. - (7) ~ (16) are cases of underflow because the left-most two bits are
10and they are different.
5.2.1 An alternative way to determine over-/underflow
This is my own observation but maybe it has been proven true or false somewhere else.
In the expression \(N_1 + N_2 = S\) where \(N_1\), \(N_2\), and \(S\) are all in two’s complement representation:
- \((N_1 > 0 \land N_2 > 0 \land S < 0) \Rightarrow Overflow\)
- \((N_1 < 0 \land N_2 < 0 \land S > 0) \Rightarrow Underflow\)
5.3 Subtraction in two’s complement
Subtraction can be implemented by adding the negative counterpart. For example:
- \((2)_{10} - (1)_{10} = (2)_{10} + (-1)_{10} = (010)_2 + (111)_2 = (001)_2 = (1)_{10}\)
- \((-1)_{10} - (2)_{10} = (-1)_{10} + (-2)_{10} = (111)_2 + (110)_2 = (101)_2 = (-3)_{10}\)
- \((1)_{10} - (-2)_{10} = (1)_{10} + (2)_{10} = (001)_2 + (010)_2 = (011)_2 = (3)_{10}\)